Hello readers, for this article I am going to explain my approach to create a forecast system of the French (metropolitan) energy consumption. This kind of problem is more or less related to part of my job at EDF Energy but this work has been done in my free time to complete my machine learning engineer nanodegree from Udacity.

In this article, there will be a description of the data used for this project, an explanation of the approach used to make a daily forecast of the consumption and the half hourly version.

Exploration of the dataset

In this case, the data to create the model are from:

RTE, the energy network manager in France they have created an open data platform to access different datasets on the network
The GEOFLA dataset that gives you information on the number of inhabitants in the city and the area
Weather underground. I have to scrape this data source from the website (I focus my scraping on the weather stations from the airports) and I pick the weather stations that have enough data during the period measured by RTE. I focus my data analytics on the outdoor temperature and the wind speed.

For the weather condition, I chose to create a national weather dataset where basically each region has its weather station associated. These stations are weighted by the number of people that are in this region (this information is coming from the GEOFLA dataset). To make the data analysis, I chose to convert the average power consumed from RTE into energy (in MWh).

In the following figure there is an illustration of the average energy consumed in France for the past years.

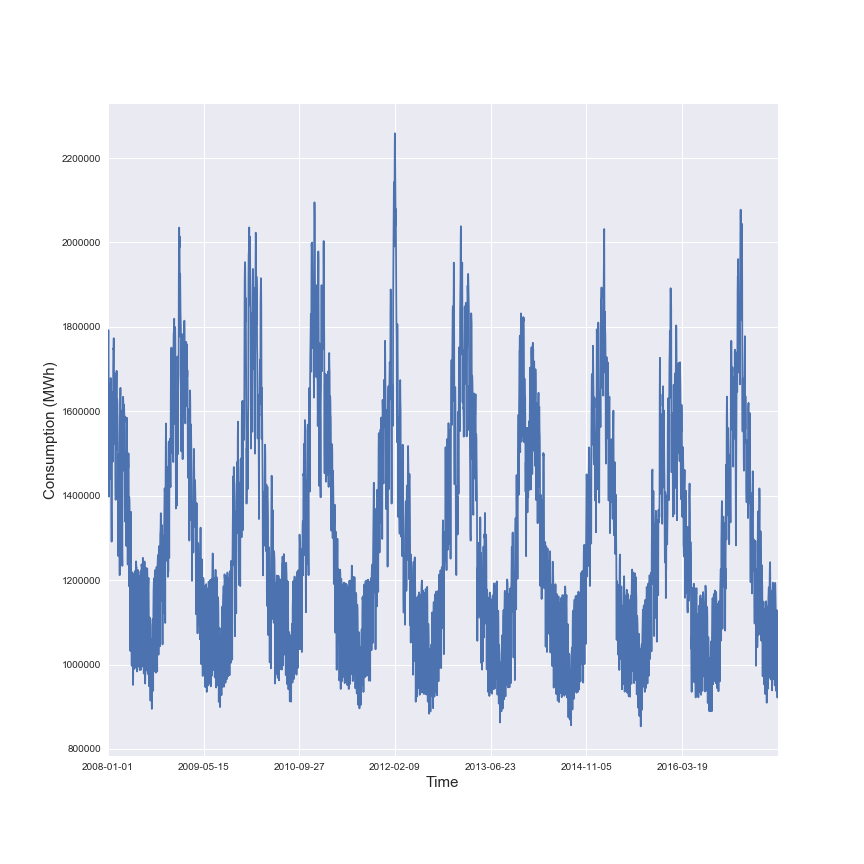
Img illustration

This figure illustrates the seasonality in the energy consumption in France.

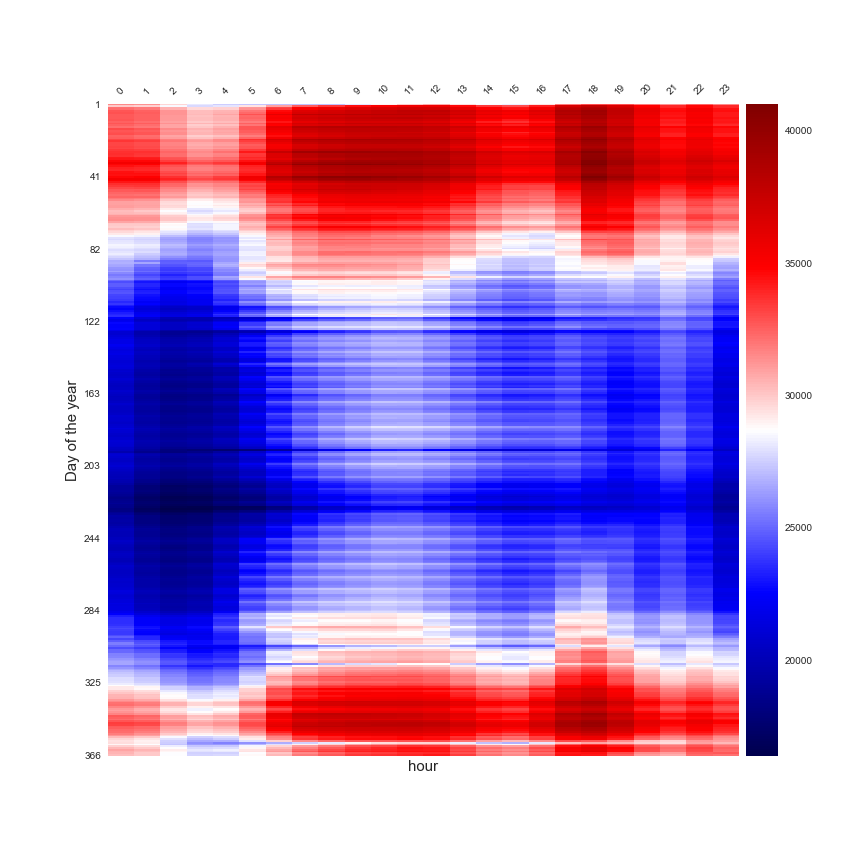
After that to make the forecast at a daily scale, I have to aggregate the data. In the following figures, there is a representation of the daily data aggregated at different scale in a heatmap.

A study of the hourly effect in function of the day of the year

Img 2 illustration

A study of the consumption of the month of the year and the day of the week.

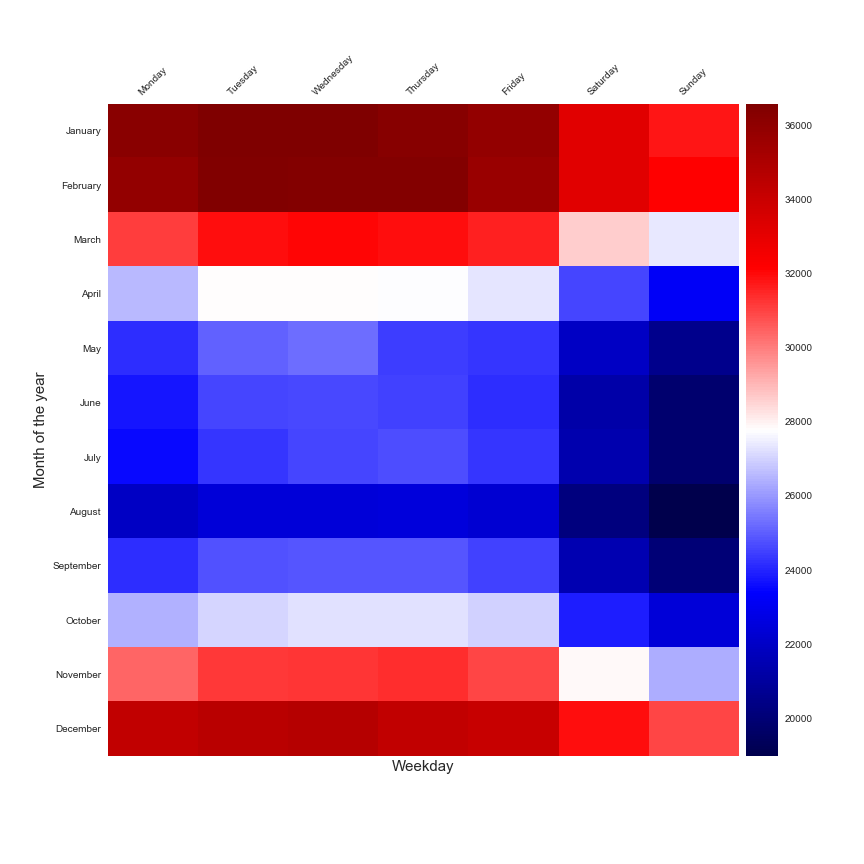
Img 3 illustration

These two figures are perfect to illustrate that the daily consumption is linked to the time of year and the day of the week. But these insights are not enough to create a forecast model. A very popular approach that is used to make a forecast of the energy consumption is the study of the daily consumption as a function of the average daily outdoor temperature. This technique is called PTG for Power Temperature Gradient and you can find a lot of publications that are based on this approach.

In the following figure there is a representation of this model used for the forecast.

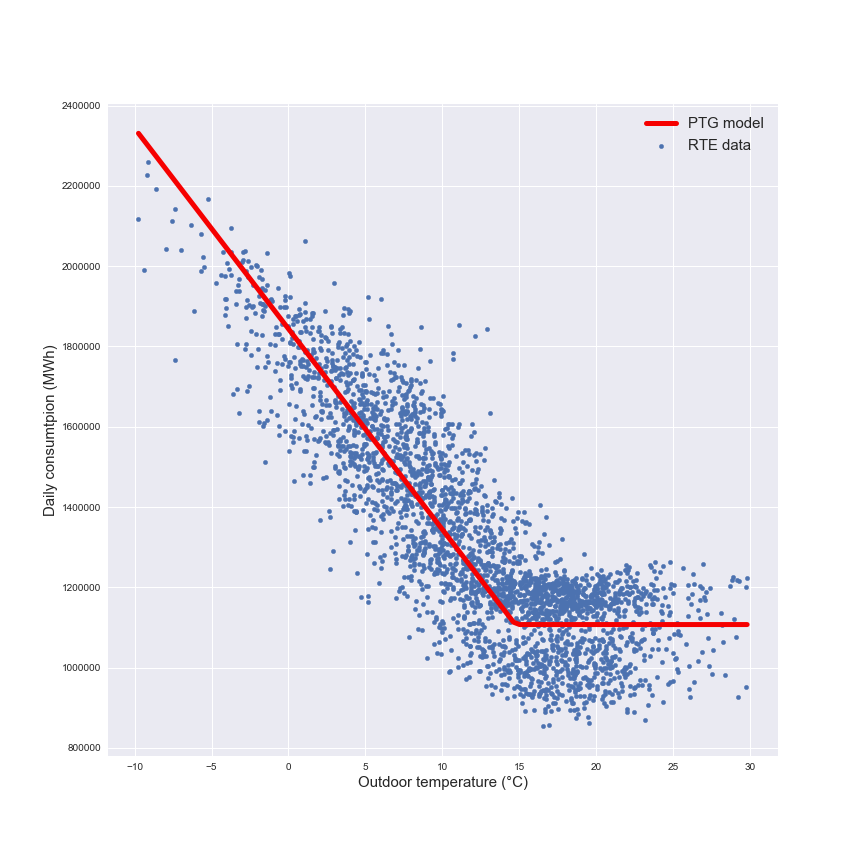
Img 4 illustration

The model is a piecewise regression with a winter part represented by the linear regression (that includes the heating needs and the appliances) and a summer part with the constant part (only the appliances). This model will be the reference model for the next part.

Daily forecast

To create the model, the dataset will be split between training set and test set, the selection of the samples for the sets will be randomized. That’s representing:

2337 samples for the training set
585 samples for the test set

This is a regression problem, so the following models from scikit learn are going to be tested:

This is a personal selection of different models and there is plenty of other models to try but for a start I think that was enough. I have to tune the different models and find the best parameters to use. I used a k-fold approach on the training set (I created ten folds) to test the different parameters. I invite you to check my report to see the choices made on the parameters for the different models.

To test the impact of the input in the models, I tested different inputs:

only outdoor temperature
outdoor temperature and wind speed
outdoor temperature and month of the year and day of the week

To facilitate the usage of the inputs I have to normalize the sets. To assess the accuracy of the model I used the r²score metric that is used for regression problems. But this metric is not enough to assess the quality of the algorithm. The second metric that I will use is the time to create the model. In the following table there is the evolution of the r²score as a function of the model used.

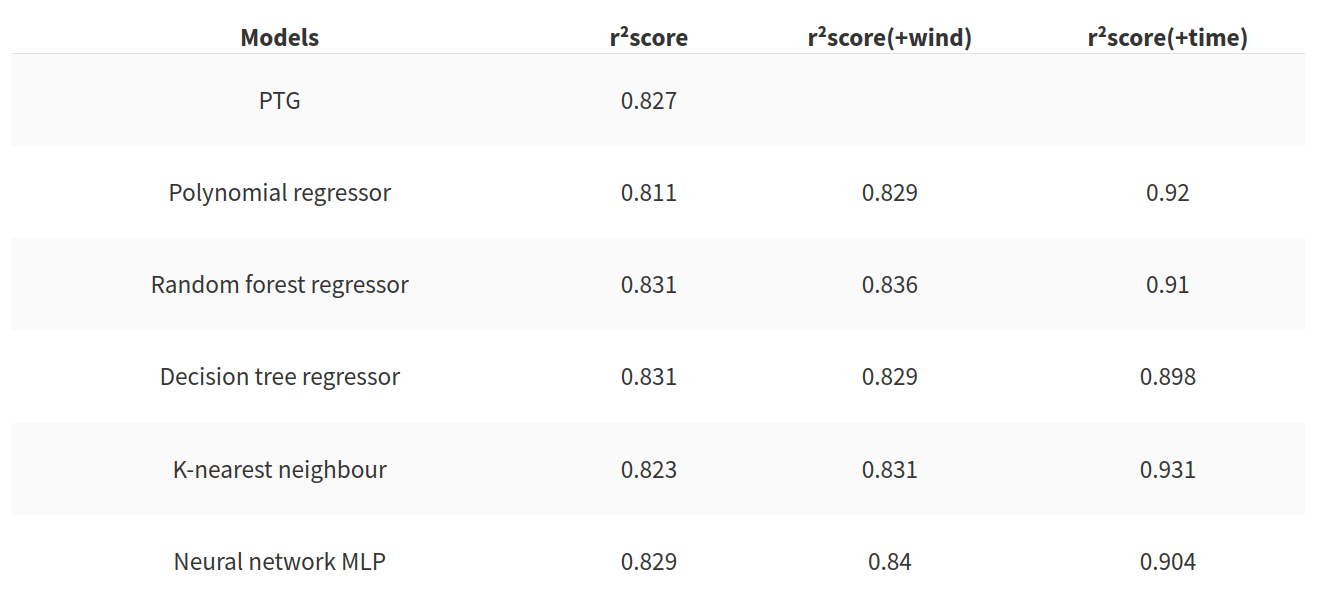
Img 5 illustration

This table allows us to draw the following conclusions:

The PTG is quite a good model. For an outdoor temperature-based only model, the score is good but the tree-based model and the neural network offer good results too
the addition of the wind speed improves the score but the gain is very small
the addition offers an interesting gain to the score for every model tested

But as I said previously the r²score is not enough, in the following table there is the time to create the model in the case of the addition of the time features to the initial inputs.

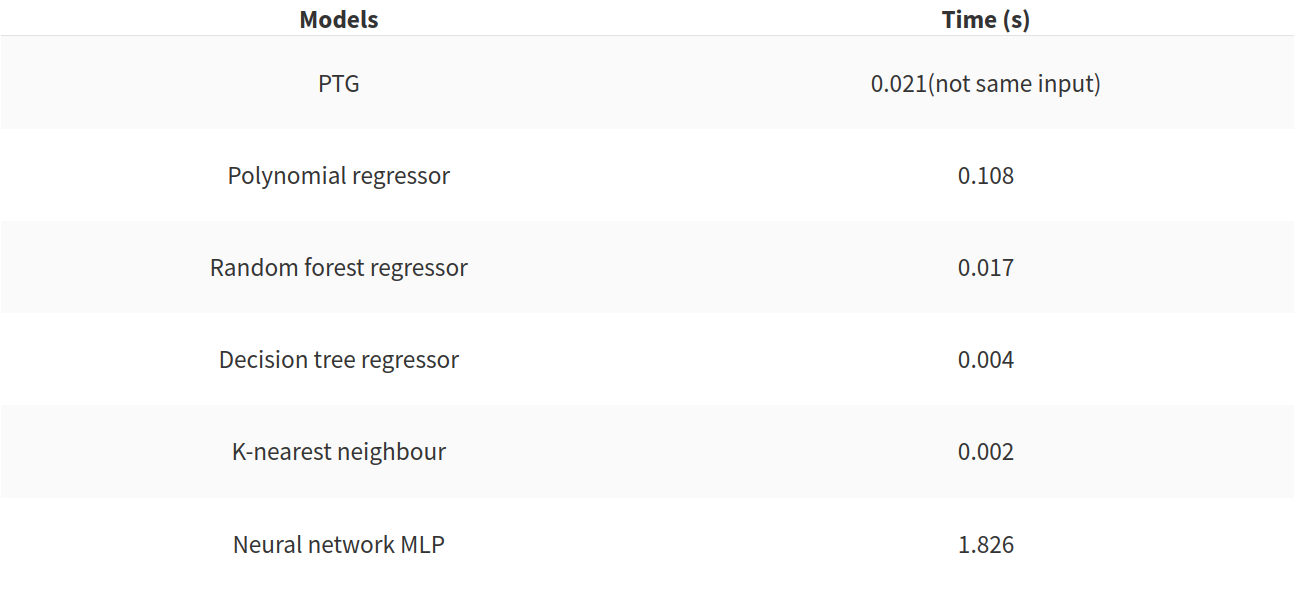
Img 7 illustration

This table is illustrating that the PTG has good performance, and that the neural network is very bad in terms of speed. The polynomial regressor should be avoided too. But these two metrics are not enough to evaluate the efficiency of the models. The impact of the size of the training set should be studied. In the following figure, there is an illustration of the impact of the training set.

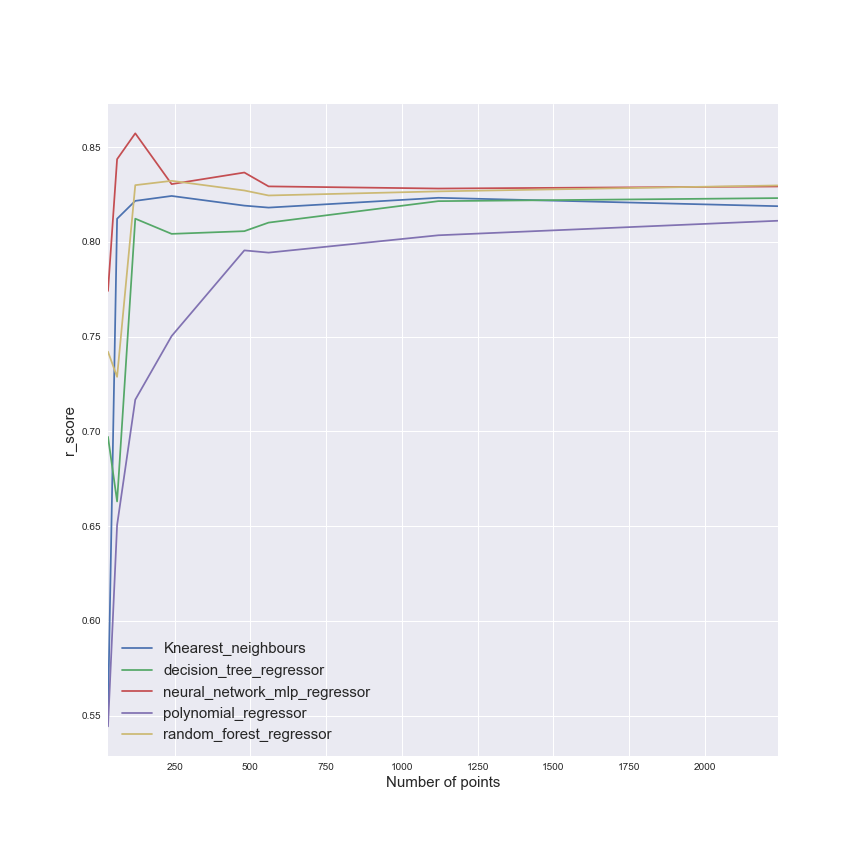
Img 8 illustration

This figure shows us that the size of the training set has a clear impact on the polynomial regressor, while other models seem less impacted (the neural network shows good efficiency quite quickly).

Half hourly forecast

For this part, we will use all the results found previously (the use of the time features essentially). I will test the same models as for the daily forecast and use the same metrics.

My benchmark model will be the ARIMA model. This model is quite popular for forecasting time series (but needs to not randomize the sets). These sets are composed of:

112176 samples for the training set
28080 samples for the test set

In my problem the results of the model are bad. In the following table there is a summary of the results of the benchmark model and the other models tested.

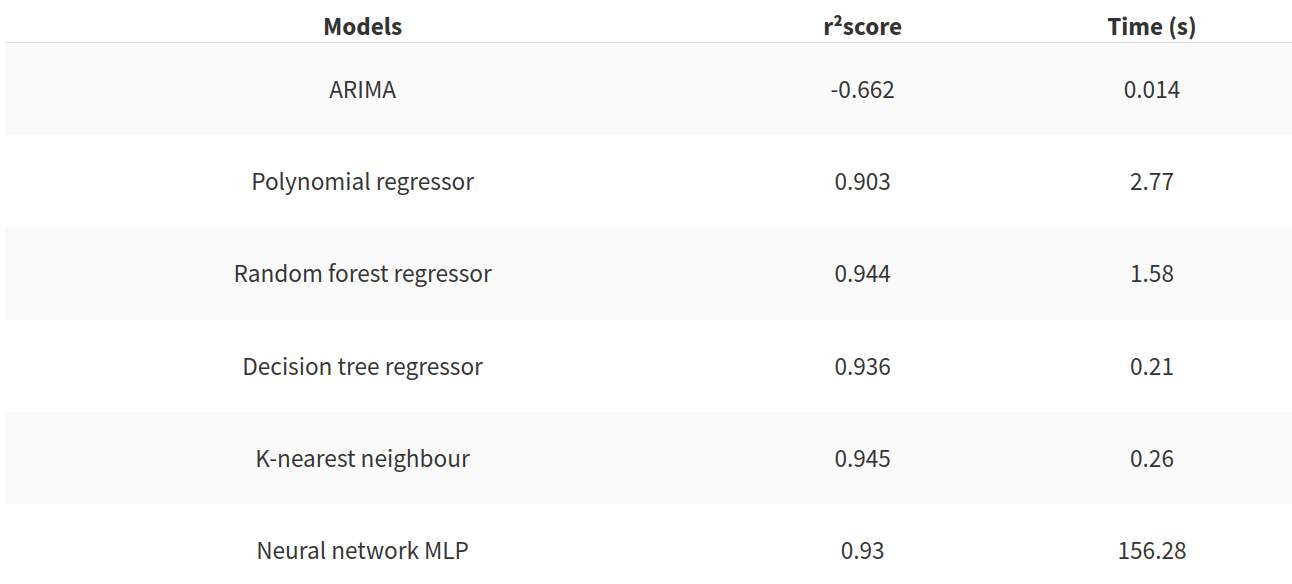
Img 9 illustration

This final table shows us that the benchmark model is quite easy to beat. The neural network is very slow to construct but two models seem very good to use for our problem:

the decision tree regressor
the K-nearest neighbour

Conclusion

This work was used to complete my nanodegree. This is my approach, not the only one, and I think there are a lot of things to try like a deep learning approach or a reinforcement learning one for example.

I invite you to use the datasets of this project to try to create your own (better?!) model and if you have any comments, write them below.