The odd dataguy
🔍
Comment la factorisation matricielle transforme les retours utilisateurs
Systèmes de Recommandation

Comment la factorisation matricielle transforme les retours utilisateurs

• 20 min de lecture

Note: Cet article a été traduit avec Claude Code le 31 janvier 2026. La version originale est disponible ici.

Récemment au travail, j’ai recommencé à utiliser l’algorithme ALS dans le package PySpark MLlib pour construire des facteurs utilisateur et item. Cet algorithme, assez célèbre dans les systèmes de recommandation, est basé sur le concept de factorisation matricielle (MF), qui est familier dans le domaine de la réduction de dimensionnalité du machine learning. J’ai pensé que discuter de la factorisation matricielle pourrait faire un bon article car c’est une technique puissante.

Cet article présentera les concepts fondamentaux de la factorisation matricielle, ainsi qu’une liste non exhaustive d’algorithmes populaires mettant en évidence leurs caractéristiques spécifiques et couvrira quelques points clés à garder à l’esprit lors de l’utilisation de la factorisation matricielle pour les systèmes de recommandation.

Les notations au cœur de la factorisation

Alors, qu’est-ce que la factorisation matricielle dans le contexte des systèmes de recommandation ? Typiquement, cela implique de prendre une matrice de notations utilisateur-item (souvent appelées feedback dans la littérature) et de la factoriser en deux matrices : une pour les utilisateurs et une pour les items (Exemple).

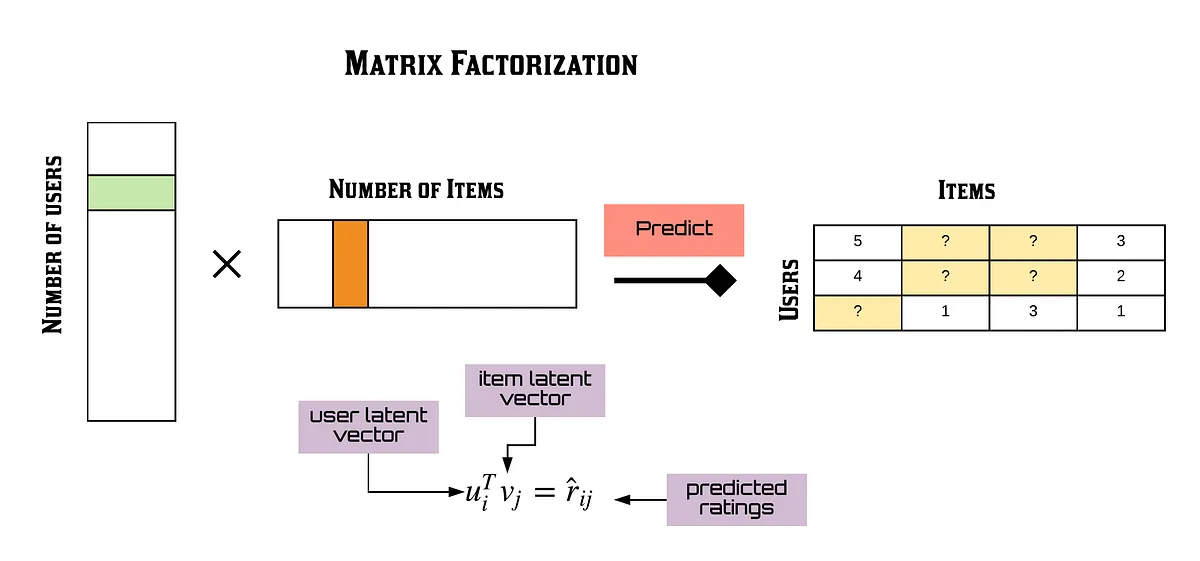
D’où viennent ces notations ?

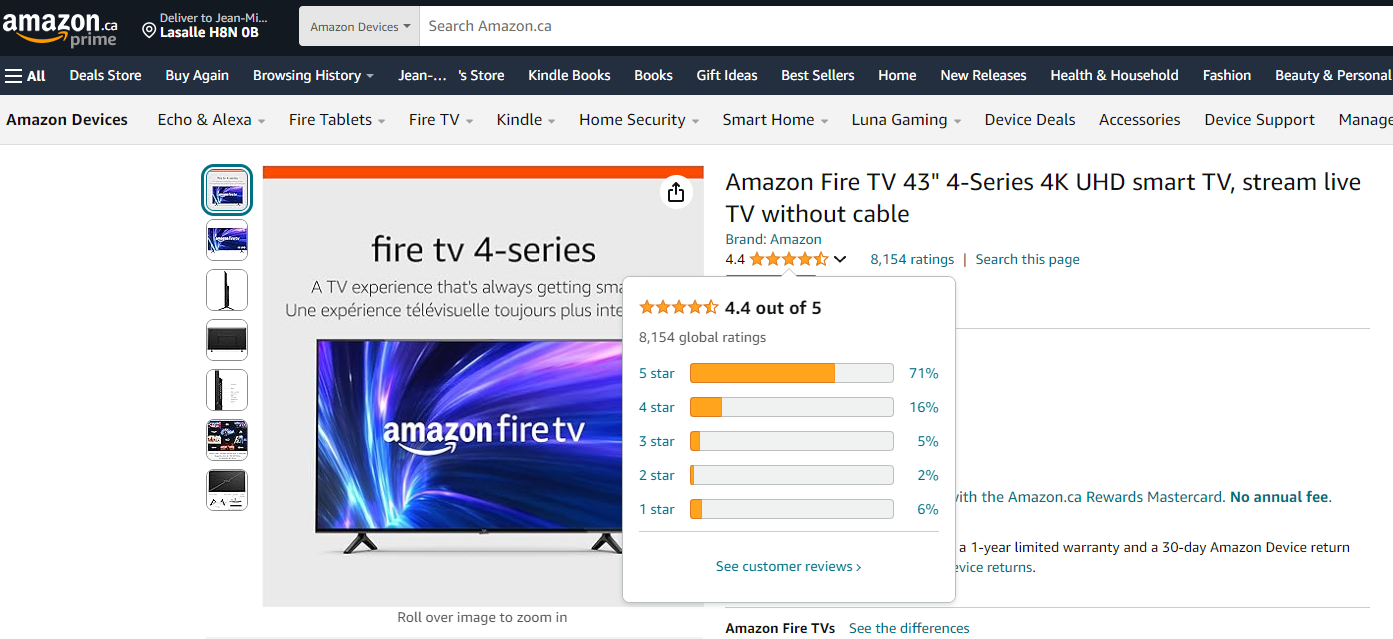
  • Explicite : Un utilisateur donne un score à un item basé sur sa préférence et sur une échelle dédiée. Un exemple célèbre est le système de notation 5 étoiles d’Amazon.

  • Implicite : Un utilisateur interagit avec les items dans le catalogue de votre application, et basé sur ces interactions, nous pouvons déterminer les préférences implicites de l’utilisateur. Par exemple, si vous regardez des séries TV sur Amazon Prime, vous pourriez en finir certaines et pas d’autres, ou vous pourriez visiter la page de contenu pour certains items mais pas d’autres. Ces interactions peuvent révéler des préférences implicites dans le catalogue.

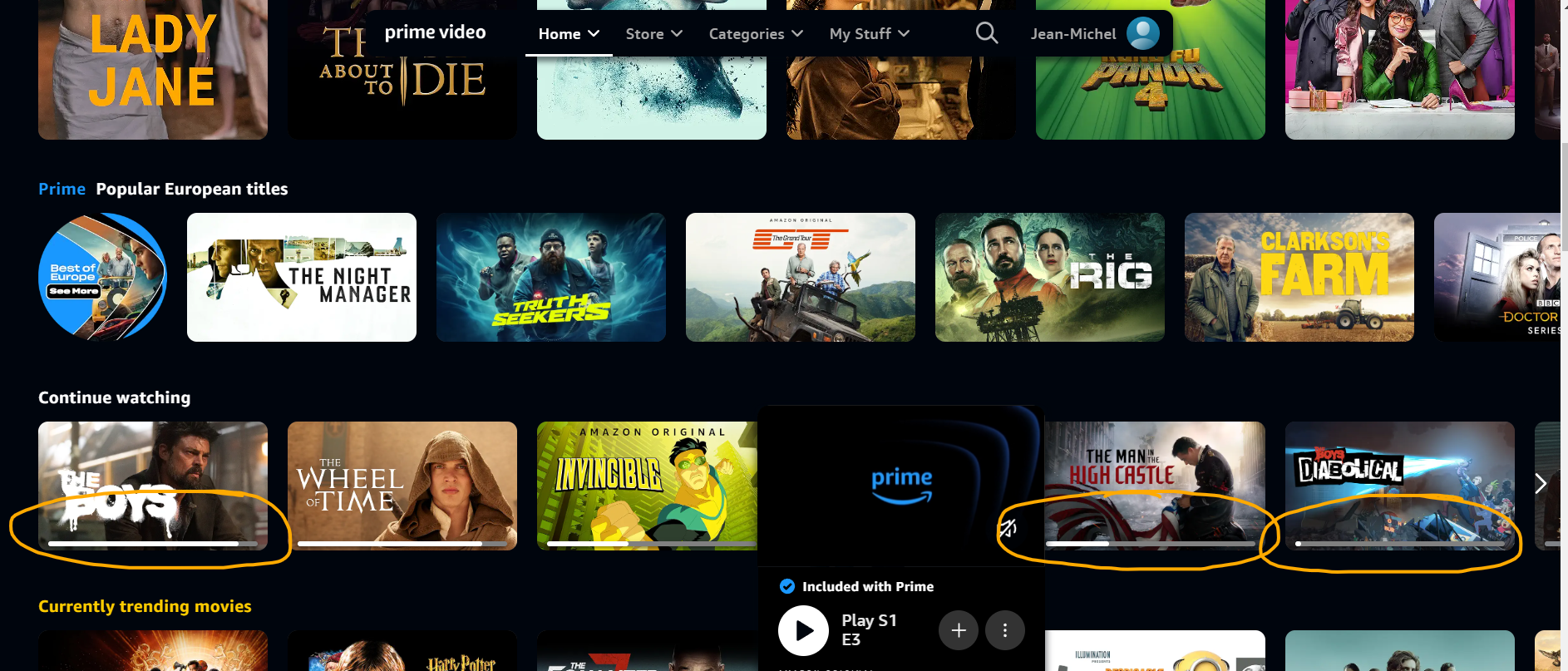
Notez que Prime Video offre également la possibilité de donner un pouce levé ou baissé au contenu dans son catalogue.

Dans les deux cas, les notations sont définies sur une échelle spécifique (par exemple, 0 à 5, 👎👍, ou 0 à 1). Elles sont construites sur les interactions utilisateur avec le catalogue, et dans toute application, la stratégie de l’entreprise peut évoluer au fil du temps. Un bon exemple de cela est Netflix. J’ai compilé quelques ressources sur la stratégie changeante de Netflix au fil du temps concernant la collecte des retours utilisateurs. Voici quelques étapes clés :

  • En 2009 : Netflix était encore une entreprise de location de DVD, donc leur système de feedback était similaire à celui d’Amazon, avec un mécanisme de notation 5 étoiles et un système de revue. Une bonne illustration de cela est l’ensemble de données pour la compétition Netflix Prize (Kaggle).

  • Vers 2016 : Netflix a déclaré publiquement que le mécanisme de notations était sous-optimal et impactait négativement le système de personnalisation, car les utilisateurs notaient souvent le contenu basé sur la “qualité” au lieu de “l’appréciation” (source).

  • En 2017-2018 : Netflix a abandonné le système de notation 5 étoiles et le mécanisme de revue en faveur d’un système pouce levé/baissé (Sources : Variety, Forbes.). Ce changement :

    • A augmenté l’engagement avec le mécanisme de notation de 200%.
    • A introduit une fonctionnalité “pourcentage de correspondance” pour mettre en évidence le contenu qui pourrait être intéressant pour les utilisateurs.

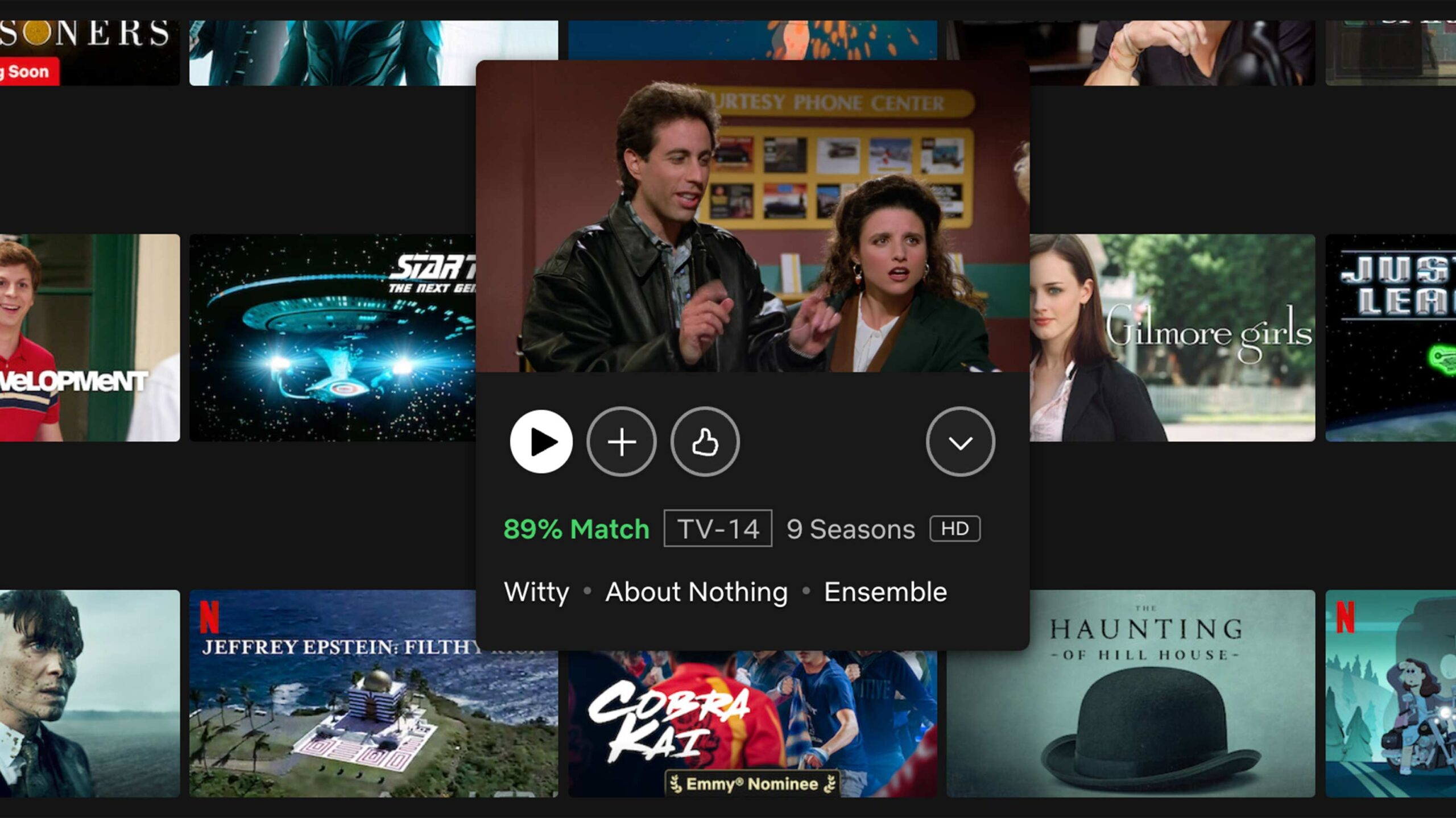
  • En 2022 : Netflix a modifié le mécanisme de pouce levé en ajoutant une option double pouce levé pour signifier un intérêt plus fort pour le contenu. Cette fonctionnalité aide à affiner les recommandations pour montrer plus de séries ou films influencés par ce que les utilisateurs adorent (source).

Netflix est un bon exemple de comment la collecte de retours utilisateurs a évolué pour personnaliser l’expérience utilisateur. Si vous êtes curieux sur les données qu’ils utilisent, vous pouvez demander un dump de données depuis le site web Netflix. Il y a plein d’informations dedans, ce qui pourrait valoir un article dédié.

Pour conclure cette section, je veux souligner que l’utilisation de cette matrice de notations implique le concept de sparsité matricielle. La sparsité matricielle peut définir la portée de la matrice en appliquant l’opération suivante :

sparsity = 1 - (number_of_ratings / (number_users * number_items))

Cette formule représente combien il y a de couverture du paysage item-utilisateur, où :

  • la sparsité proche de 1 signifie que la plupart des utilisateurs n’ont pas interagi avec les items (une matrice sparse).
  • la sparsité proche de 0 signifie que la plupart des items ont été interagis par les utilisateurs (une matrice dense).

Dans les cas d’usage réels, la sparsité peut être assez élevée selon l’application. Il est important de garder ce nombre à l’esprit, car il peut impacter la sélection des techniques pour la factorisation matricielle. Plongeons dans les différentes techniques disponibles pour cette factorisation.

Techniques de factorisations matricielles

Comme je l’ai mentionné plus tôt, la factorisation matricielle est liée au concept de réduction de dimensionnalité. Son rôle est de réduire la taille de la matrice originale en la décomposant en sous-matrices—une pour les utilisateurs et une pour les items. Mais pourquoi faire cela ?

Avec ces sous-matrices, vous pouvez estimer la notation ou le feedback spécifique d’un utilisateur pour un item particulier. Cela se fait en sélectionnant le vecteur d’un utilisateur (une ligne ou colonne dans la matrice utilisateur) et le vecteur d’un item (une ligne ou colonne dans la matrice item) et en effectuant une opération, généralement un produit scalaire, bien que d’autres méthodes puissent également être utilisées.

En effectuant cette opération, vous pouvez évaluer comment la factorisation a fonctionné en comparant les notations prédites aux notations réelles. De plus, cette méthode peut estimer un score pour des paires utilisateur/item qui n’ont pas été vues auparavant, basé sur la distribution générale des notations dans la matrice originale et les motifs extraits pendant la factorisation. La factorisation est considérée comme complète lorsque, au fil du temps, le processus minimise l’erreur entre les notations réelles et les estimées.

Il existe de nombreux algorithmes disponibles pour la factorisation matricielle, mais quelques-uns sont plus adaptés aux systèmes de recommandation, car ceux-ci impliquent généralement une factorisation de matrice sparse. Nous explorerons les principaux algorithmes pour ce type d’application dans les sections à venir (en quelque sorte dans un ordre chronologique).

Décomposition en valeurs singulières (SVD)

Origine : SVD est une technique qui semble avoir apparu dans sa première forme à la fin du 19e siècle (par Eugenio Beltrami et Camille Jordan), mais sa forme plus moderne de calcul réalisée par Gene Golub et William Kahan a été publiée dans les années 1960 et 1970 (basé sur les méthodes). À la fin des années 1990, SVD est devenu de plus en plus populaire dans le traitement d’image et le domaine des systèmes de recommandation.

Principe : Si vous voulez apprendre sur toute l’algèbre linéaire sous le capot, la page Wikipedia a de bonnes références dedans, mais globalement l’idée est de décomposer les matrices originales en trois sous-matrices.

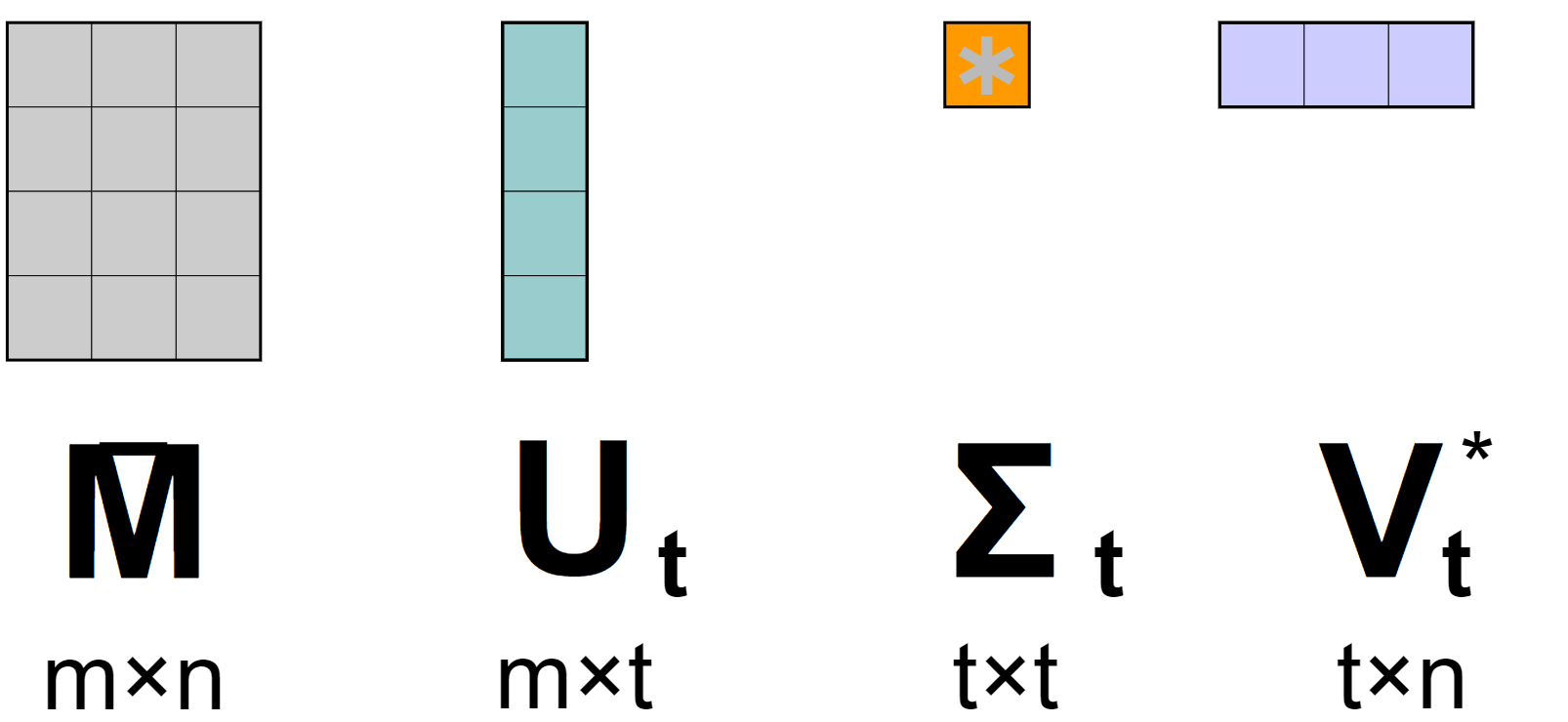
Basé sur la version du SVD (complet, compact, tronqué, mince), les dimensions des matrices de sortie peuvent varier (et cela peut rendre le SVD plus ou moins applicable car vous pouvez rencontrer des problèmes de scalabilité)

Actuellement, une des versions les plus communes de SVD utilisée est la tronquée, et depuis le début des années 2000, nous avons vu l’apparition de SVD dédiés pour les systèmes de recommandation avec, par exemple, SVD++ qui est conçu pour factoriser des matrices de feedbacks implicites.

Factorisation matricielle non-négative (NMF)

Origine : NMF est une technique qui est apparue dans les années 1990 et a été développée à l’origine par un groupe de chercheurs finlandais, mais popularisée par l’investigation de Lee et Seung de Samsung en 1999.

Principe : Le processus global est de décomposer la matrice originale en deux sous-matrices avec la matrice de Feature et la matrice de Coefficient.

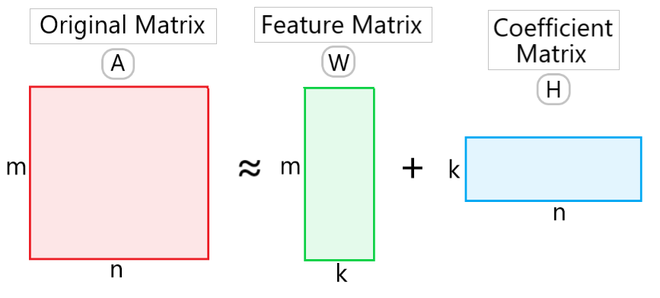
Le processus commence par initialiser W et H avec des valeurs aléatoires non-négatives. Par un processus itératif, ces matrices sont mises à jour pour minimiser la différence entre A et le produit W×H. Les mises à jour sont effectuées en utilisant des règles multiplicatives qui garantissent que tous les éléments restent non-négatifs.

Factorisation matricielle de Funk

Origine : La factorisation matricielle de Funk a été popularisée par Simon Funk lors de la compétition Netflix Prize en 2006. Elle est devenue largement connue pour sa simplicité et son efficacité dans l’amélioration de la précision des systèmes de recommandation.

Principe : La factorisation matricielle de Funk décompose la matrice d’interaction utilisateur-item en deux matrices de dimensions inférieures, représentant des facteurs latents pour les utilisateurs et les items. L’objectif est de prédire les entrées manquantes dans la matrice originale en minimisant l’erreur de prédiction des interactions connues. Funk MF exploite la descente de gradient stochastique (SGD) pour mettre à jour itérativement les matrices de facteurs latents, optimisant l’approximation de la matrice originale (cela ressemble à un SVD mais pas vraiment, donc vous pouvez le trouver dans la littérature sous le nom de funk SVD)

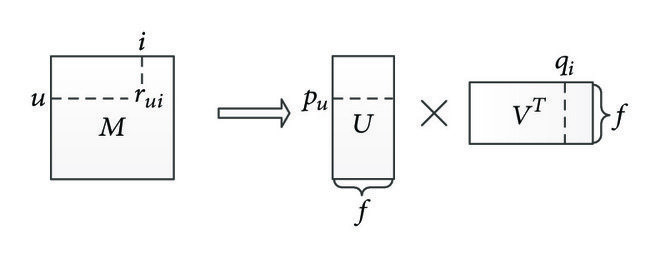
Factorisation matricielle probabiliste et bayésienne

Origine : La factorisation matricielle probabiliste (PMF) et sa variante bayésienne (BMF) ont été introduites pour aborder les problèmes d’incertitude et de sparsité dans les systèmes de recommandation. PMF a été popularisée par Ruslan Salakhutdinov et Andriy Mnih en 2008.

Principe : La factorisation matricielle probabiliste modélise la matrice d’interaction utilisateur-item comme un produit de deux matrices de dimensions inférieures. Chaque entrée dans la matrice originale est traitée comme une distribution gaussienne, permettant l’incertitude dans les prédictions. Le modèle vise à minimiser l’erreur de reconstruction en ajustant les matrices de features latentes par estimation du maximum de vraisemblance.

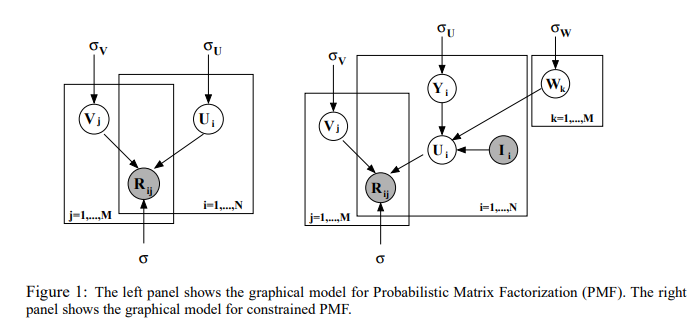
La factorisation matricielle bayésienne étend PMF en incorporant des distributions a priori sur les facteurs latents. Cette approche bayésienne fournit un cadre plus flexible en capturant l’incertitude dans les paramètres du modèle. En utilisant des techniques comme les chaînes de Markov Monte Carlo (MCMC) ou l’inférence variationnelle, BMF infère les distributions postérieures des facteurs latents, résultant en une estimation plus robuste surtout lors du traitement de données sparse.

Moindres carrés alternés (ALS)

Origine : L’algorithme ALS est une approche populaire pour le filtrage collaboratif dans les systèmes de recommandation. Il a gagné en importance au début des années 2000, notamment utilisé dans la compétition Netflix Prize pour améliorer les recommandations de films.

Principe : L’algorithme ALS est utilisé pour la factorisation matricielle, où l’objectif est de décomposer une matrice d’interaction utilisateur-item en deux matrices de dimensions inférieures : la matrice utilisateur-feature et la matrice item-feature. L’idée clé est d’optimiser itérativement une matrice tout en gardant l’autre fixée, en alternant entre les deux jusqu’à convergence.

Il est particulièrement bien adapté aux environnements de calcul distribué en raison de l’indépendance des mises à jour de chaque utilisateur ou item, permettant la parallélisation. Cela en fait un choix robuste pour les systèmes de recommandation à grande échelle.

Machines de factorisation (FM)

Origine : Les machines de factorisation ont été introduites par Steffen Rendle en 2010 pour gérer les données sparse et capturer des interactions complexes entre les variables. Elles ont été développées pour améliorer la précision de prédiction dans les systèmes de recommandation et autres tâches impliquant des données de haute dimension.

Principe : Les machines de factorisation combinent les forces des modèles linéaires avec la factorisation matricielle pour modéliser les interactions entre les features. L’idée clé est de représenter ces interactions par des paramètres factorisés, ce qui permet au modèle de capturer efficacement des relations complexes dans les données.

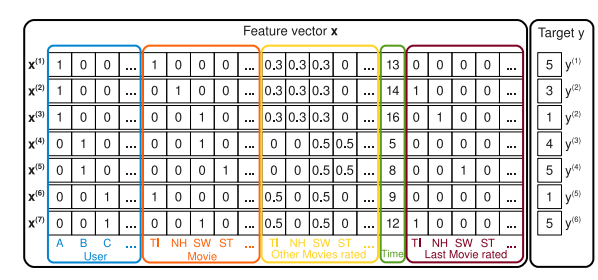
Les FM peuvent modéliser toutes les interactions entre les variables en les représentant comme le produit intérieur de vecteurs de facteurs latents, les rendant hautement flexibles. Cette approche permet aux FM d’apprendre des interactions sans les définir explicitement, permettant des prédictions scalables et précises même avec des ensembles de données sparse.

Factorisation matricielle basée sur le deep learning

Origine : La factorisation matricielle basée sur le deep learning a émergé comme une extension naturelle des techniques traditionnelles de factorisation matricielle, incorporant des réseaux de neurones pour modéliser des interactions complexes dans les données. Cette approche a gagné en traction dans les années 2010 avec la disponibilité accrue des ressources de calcul et les avancées dans les architectures de réseaux de neurones, particulièrement pour les systèmes de recommandation.

Principe : La factorisation matricielle basée sur le deep learning améliore la factorisation matricielle traditionnelle en utilisant des réseaux de neurones pour apprendre des relations non-linéaires entre les utilisateurs et les items. Contrairement aux approches classiques, qui décomposent une matrice en combinaisons linéaires de facteurs latents, les méthodes de deep learning utilisent des réseaux de neurones pour capturer des motifs plus complexes.

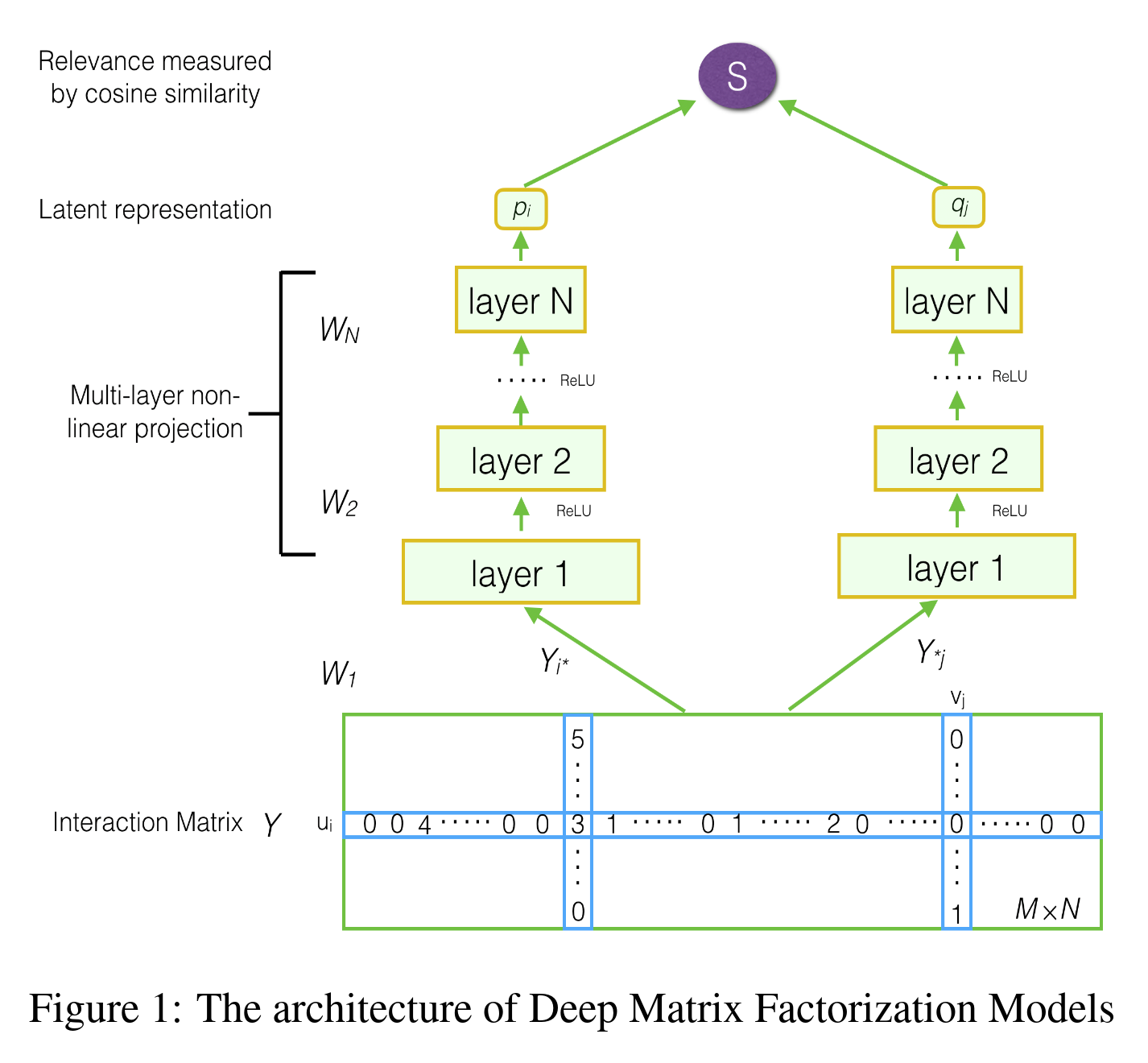
Par exemple, l’article Neural Collaborative Filtering de Xiangnan He et collègues de 2017 est très populaire. Ils utilisent un perceptron multi-couches (qui remplace le produit scalaire) pour effectuer la factorisation. Des techniques récentes comme l’autoencodeur variationnel peuvent également être utilisées pour réduire les dimensions et construire des facteurs de manière différente, mais très efficace. Il y a une bonne illustration dans cet article avec des références utiles.

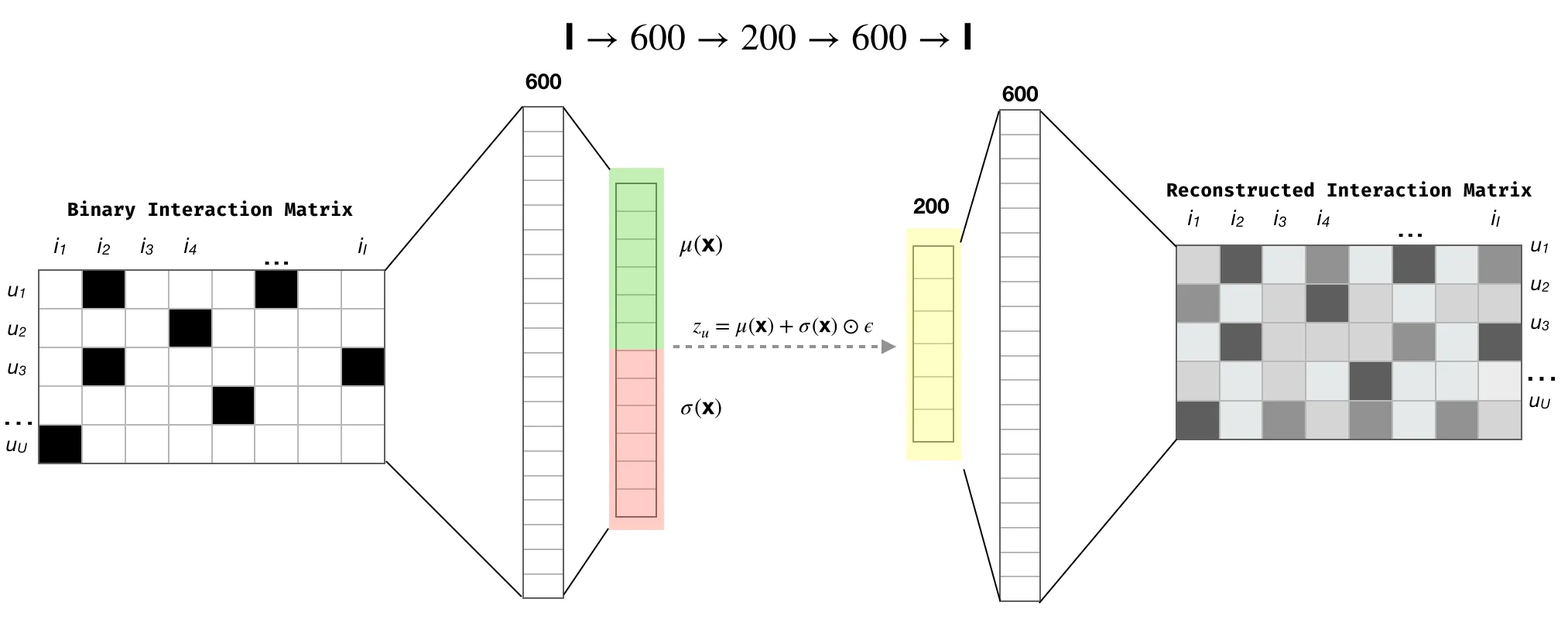
Donc, c’était mon aperçu général de la factorisation matricielle pour les systèmes de recommandation. Maintenant, plongeons dans quelques considérations à garder à l’esprit lors du travail avec ces techniques.

Considérations autour de la MF

Indexer les notations

Une des étapes les plus basiques avant d’appliquer toute technique de factorisation matricielle est d’indexer les identifiants utilisateur et item dans les indices de la matrice de notations.

Il existe plusieurs façons de faire cela. En Python, vous pouvez facilement utiliser les fonctions pandas pour l’indexation. Cependant, pour quelque chose de plus scalable dans un environnement de production (utilisant Spark par exemple), je préfère :

  • Construire des tables de mapping pour les utilisateurs et les items à mesure qu’ils apparaissent pour la première fois dans l’écosystème de l’application. Ce processus devrait être incrémental pour maintenir l’efficacité.
  • Pour associer des indices, voici un extrait rapide de code en PySpark que je trouve utile :

Maintenant que nous avons ce mapping disponible, plongeons plus profondément dans par où commencer avec la factorisation matricielle.

Par où commencer ?

Voici mes deux recommandations pour commencer la factorisation matricielle dans le contexte des recommandations :

  • Pour une configuration locale ou mono-machine, le package Surprise est définitivement l’endroit où commencer. Ce package est construit sur scikit-learn et implémente plusieurs algorithmes mentionnés dans les sections précédentes (SVD, NMF, etc.).

Voici une présentation rapide :

  • Pour une approche plus distribuée, PySpark MLlib a une implémentation de l’algorithme ALS qui est très complète. Elle vous permet de configurer des modes pour exécuter avec du feedback implicite ou imposer des facteurs non-négatifs dans les sous-matrices.

Je crois que ces deux packages fournissent un bon point de départ pour quiconque cherchant à utiliser la factorisation matricielle pour les recommandations.

Échantillonnage négatif comme augmentation de données

Dans divers articles et implémentations, le processus d’échantillonnage négatif est mentionné comme un moyen d’ajouter de nouvelles données à l’ensemble d’entraînement. Cette opération est utilisée dans le contexte de feedback implicite, où l’objectif est d’ajouter des interactions négatives. Dans les scénarios avec feedback implicite, vous avez souvent seulement du feedback positif (comme des clics, ou des transactions), donc l’échantillonnage négatif aide à aborder le déséquilibre en ajoutant un contrepoids, améliorant l’apprentissage de motifs dans la matrice de notations.

Il existe différentes stratégies pour implémenter l’échantillonnage négatif :

  • Choisir des items aléatoires pour être étiquetés comme négatifs.
  • Choisir des items basés sur la popularité (les items plus populaires ont une chance plus élevée d’être étiquetés négatifs car l’utilisateur a choisi de ne pas interagir avec eux).

Pour moi, cette technique devrait être traitée comme un “hyperparamètre” pour les données derrière la factorisation matricielle, un outil très puissant à utiliser avec les bonnes précautions car vous pouvez injecter des biais dans vos données.

Évaluation

Pour ce problème, évaluer la qualité des notations prédites est crucial. Utiliser RMSE ou toute autre métrique liée à la régression fera le travail. De plus, évaluer les capacités de classement de l’algorithme est intéressant. Une bonne approche pour votre ensemble de test est la suivante :

  • Pour chaque utilisateur dans votre ensemble de test, choisissez aléatoirement X items (par exemple, 100).
  • Prédisez la notation pour chaque paire utilisateur-item sélectionnée.
  • Faites de même pour chaque item dans l’ensemble de test pour cet utilisateur.
  • Évaluez les métriques de classification (comme Hit Ratio ou NDCG) en comparant le classement des items de l’ensemble de test avec les items sélectionnés aléatoirement. Pour les notations positives, vous attendriez qu’elles se classent plus haut sur la liste.

Cette méthode est efficace pour évaluer la capacité de classement de la factorisation matricielle, mais elle nécessite une sélection prudente des items.

Scalabilité

C’est une considération majeure quand vous voulez industrialiser ce type d’algorithmes. J’ai trois règles à garder à l’esprit.

Première règle : Ne construisez pas la matrice de notations ! Ou du moins, ne la construisez pas comme une matrice classique/dense, car vous auriez besoin de stocker une matrice avec des milliers de colonnes en mémoire. La meilleure approche est d’exploiter le format de matrice sparse, qui peut être offert par des packages comme Scipy ou Cupy.

J’ai benchmarké la taille mémoire d’une matrice dense (format classique) versus une matrice sparse avec différentes configurations d’utilisateurs, items et sparsité.

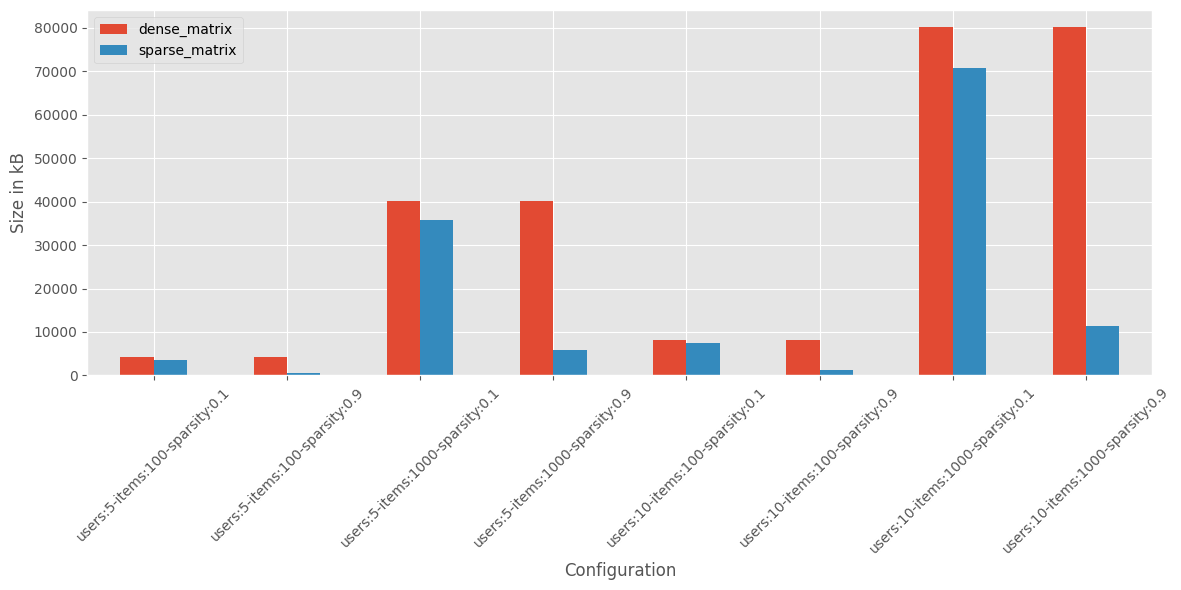
Dans les configurations avec haute sparsité, la matrice sparse peut être 6 à 7 fois plus petite en mémoire que la dense donc le format sparse est très efficace.

Deuxième règle : Réduisez l’échelle des utilisateurs et des items !

Vous n’avez pas besoin d’inclure tous les utilisateurs. Les utilisateurs avec de faibles niveaux d’interaction peuvent ajouter du bruit, fournissant peu de valeur. Avoir un seuil minimum de notations pour l’inclusion dans la matrice est un bon paramètre à garder à l’esprit (cela impactera aussi le processus d’évaluation). Cette approche est également discutée dans certains articles (1, 2) sur les systèmes de recommandation.

Dans certaines applications comme Goodreads, les utilisateurs ont besoin d’un nombre minimum d’interactions avant que les recommandations ne soient générées (pas sûr s’ils utilisent une factorisation matricielle sous le capot)

Comme avec les utilisateurs, il peut ne pas être nécessaire d’inclure tous les items, surtout ceux avec de faibles interactions (bien que ceux-ci devraient être gérés différemment). En général, ma suggestion est que vous devriez potentiellement exécuter la factorisation matricielle sur un sous-ensemble du catalogue d’items. Ce sous-ensemble devrait partager quelque chose en commun, comme la même catégorie de film ou une période de sortie spécifique.

Jouer avec ces éléments d’utilisateurs et d’items, impactera vos stratégies de cold start aka comment gérer l’utilisateur ou l’item avec un manque d’interactions parce qu’ils sont nouveaux ou pas si actifs, donc faites attention.

Ne l’utilisez pas pour faire des recommandations (directement)

Cela peut sembler bizarre, mais laissez-moi expliquer :

  • La plage des notations prédites peut ne pas correspondre à la vraie plage possible de notations. La factorisation pourrait ne pas réduire suffisamment l’erreur, et les minima locaux pourraient impacter les mécanismes de notation. Il est essentiel de construire des garde-fous lors de l’utilisation des notations prédites.
  • Certains frameworks offrent des méthodes préconstruites sur la factorisation, comme RecommendProductForUsers dans PySpark. Ces fonctions fonctionnent, mais elles peuvent ne pas gérer des conditions spécifiques que vous pourriez rencontrer lors de la construction de recommandations (et ne se mettent pas à l’échelle bien)

Par exemple, quand j’utilise ALS, je préfère construire ma propre fonction de recommandation avec des facteurs item diffusés à travers les executors.

Cette configuration fonctionne bien quand votre dataframe de facteurs item n’est pas trop grand (milliers d’items), et elle offre la flexibilité d’appliquer certaines règles personnalisées comme la pondération ou le filtrage pour des items spécifiques facilement.

Concluons maintenant l’article.

Notes de conclusion

Les notations et la factorisation matricielle sont des outils puissants pour les systèmes de recommandation. Vous pouvez les utiliser pour calculer des features utilisateur et item qui peuvent être exploitées plus tard pour recommander du contenu. Ces features peuvent être facilement intégrées pour construire des fonctionnalités d’entités liées dans votre application, comme une fonctionnalité “items similaires”.

Concernant les notations et le feedback, je recommande fortement d’utiliser différents types. Si vous avez des notations explicites, utilisez-les telles quelles, mais vous devriez aussi construire de nouvelles notations implicites pour capturer des aspects spécifiques de votre application. Par exemple, si vous avez des données de clics sur des tuiles dans votre application (en plus des notations explicites), vous devriez utiliser ces données comme input pour un nouveau système de notation qui reflète le comportement utilisateur lié aux clics. Vous pouvez combiner différents inputs pour construire ces notations, mais évitez de créer une seule notation qui essaie d’englober tout. Considérez que :

  • De nouvelles données de tracking peuvent émerger et altérer votre compréhension de votre application.
  • Il deviendra plus difficile d’expliquer la source de cette notation, la rendant moins utile pour l’analyse et la compréhension.

Différentes notations (et les matrices factorisées associées) aideront à résumer les préférences d’un utilisateur basées sur leurs interactions.

Quand il s’agit de choisir le bon algorithme, cela dépend vraiment de :

  • Les notations utilisées : Le type et la plage des notations influenceront quels algorithmes vous pouvez utiliser (comme SVD vs. SVD++).
  • Le nombre d’utilisateurs et d’items : L’échelle de vos données peut impacter la sélection d’algorithmes.
  • La sparsité de votre ensemble de données : Le ratio d’items par rapport aux utilisateurs affecte les ressources de calcul requises et peut influencer votre choix d’algorithmes.

J’ai remarqué que la sélection d’algorithmes est toujours un sujet brûlant lors des conférences sur les systèmes de recommandation. Par exemple, dans cet article de 2020 de Google, ils ont benchmarké Neural Collaborative Filtering vs. MF, où le NCF existe depuis quelques années maintenant. Encore une fois, cela dépend vraiment de votre cas d’usage, donc vous devriez les benchmarker dans votre propre environnement avant de prendre une décision.

Enfin, si vous êtes intéressé à en apprendre plus, voici quelques ressources qui pourraient être utiles :

J’espère que vous appréciez votre lecture. De mon côté, j’utiliserai ce travail comme point de départ pour de futurs projets/articles qui se concentreront plus sur :

  • Comment concevoir une fonctionnalité d’item lié de zéro
  • Comment représenter les facteurs pour les humains (spoiler : il y a, encore une fois, de la réduction de dimensionnalité impliquée)

Donc restez à l’écoute 😉

Au-delà de cet article, j’aime discuter de données, d’IA et de conception de systèmes—comment les projets sont construits, où ils réussissent et où ils échouent. Si vous voulez échanger des idées, remettre en question des hypothèses ou parler de vos propres projets, n’hésitez pas à me contacter. Je suis toujours ouvert pour une bonne conversation.